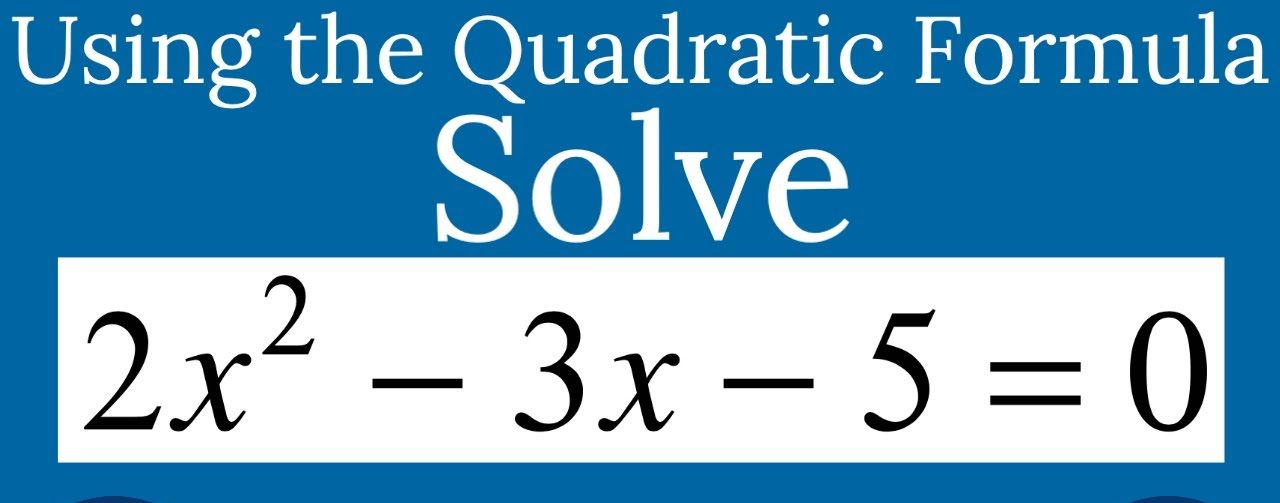In the fascinating world of mathematics, quadratic equations stand as one of the fundamental concepts that bridge simple algebraic principles and more complex mathematical theories. A quadratic equation is a second-degree polynomial typically represented in the form (ax^2 + bx + c = 0), where (a), (b), and (c) are constants, and (a \neq 0). These equations are ubiquitous in various fields, ranging from physics and engineering to economics and natural sciences.
In this article, we delve into the intricacies of solving a specific quadratic equation: (2x^2 – 3x – 5 = 0). This equation, though seemingly straightforward, encapsulates the essence of quadratic problem-solving and offers a window into the techniques used to find its roots. We will explore not only the methods to solve such equations but also the underlying principles that make these solutions so integral to understanding and predicting the behavior of natural and man-made systems.
Our journey through this equation will take us through different mathematical landscapes, from the simplicity of basic algebra to the elegance of the quadratic formula. Whether you are a student grappling with algebra for the first time, a teacher seeking fresh perspectives, or a curious mind interested in the beauty of mathematics, this exploration will provide insights into the timeless art of solving quadratic equations.
Background Theory
As we embark on the journey to solve the quadratic equation (2x^2 – 3x – 5 = 0), it is essential to lay a solid foundation by understanding the background theory of quadratic equations. This understanding not only aids in solving the equation at hand but also enriches our broader mathematical knowledge.
1. Understanding Quadratic Equations
A quadratic equation is a second-degree polynomial equation of the form (ax^2 + bx + c = 0), where (x) represents an unknown variable, and (a), (b), and (c) are coefficients with (a \neq 0). The term ‘quadratic’ originates from ‘quadra’, which means square, as the equation involves the square of the variable (x).
2. Nature of Quadratic Equations
The solutions of a quadratic equation are known as the ‘roots’ of the equation. These roots can be:
- Real and Distinct: If the equation has two different solutions.
- Real and Equal: If the equation has one repeated solution.
- Complex or Imaginary: If the equation has no real solution.
The nature of these roots is determined by the discriminant, (D), given by (D = b^2 – 4ac). Depending on the value of (D), we can predict the nature of the roots:
- If (D > 0), the roots are real and distinct.
- If (D = 0), the roots are real and equal.
- If (D < 0), the roots are complex or imaginary.
3. Methods of Solving Quadratic Equations
Several methods exist for solving quadratic equations, each with its unique approach and application:
- Factoring: This involves expressing the quadratic equation as a product of two linear factors. This method is most effective when the equation can be easily factorized.
- Completing the Square: This method involves rearranging the equation and completing the square to solve for (x). It is a more universal method but can be more complex in calculation.
- Quadratic Formula: Perhaps the most powerful and generalized method, it involves using the formula (x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}) to find the roots of the equation. This method can be used for any quadratic equation and is particularly useful when the equation is not easily factorizable.
4. Significance in Mathematical Context
Quadratic equations are more than just mathematical curiosities; they are essential tools in various fields. They model numerous physical phenomena, such as projectile motion and the behavior of certain electronic circuits. In finance, they can be used to model profit and loss scenarios. Their versatility and applicability make them a cornerstone of algebra and beyond.
In summary, understanding the background theory of quadratic equations provides the necessary context and tools to tackle not just the equation (2x^2 – 3x – 5 = 0) but also a myriad of other problems in mathematics and related fields. This foundation is crucial for both solving specific equations and appreciating the broader applications of quadratic equations in the real world.
Method Selection
In our exploration of solving the quadratic equation (2x^2 – 3x – 5 = 0), choosing the most efficient and appropriate method is crucial. While there are several techniques at our disposal, including factoring, completing the square, and using the quadratic formula, we will select the quadratic formula for this specific equation. This decision is based on a few key considerations:
1. Complexity of Factoring
Factoring is often the first method considered due to its straightforward approach. However, the equation (2x^2 – 3x – 5 = 0) does not easily lend itself to simple factoring. The coefficients are not particularly conducive to quick factorization, and there is no clear immediate factor pair that sums to -3 while multiplying to -10 (the product of 2 and -5). Attempting to factor this equation might be more time-consuming and less straightforward than other methods.
2. Completing the Square: A More Complex Alternative
Completing the square is a versatile method that can always be applied to quadratic equations. However, it involves several steps that can introduce complexity, especially for students or individuals less comfortable with algebraic manipulations. In the case of our equation, the process would require dividing by the leading coefficient (2) and completing the square, which involves fractions and additional steps that might complicate the solution process.
3. Efficiency of the Quadratic Formula
The quadratic formula, (x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}), is a universally applicable method that can solve any quadratic equation, regardless of the coefficients involved. For our equation, (2x^2 – 3x – 5 = 0), applying the quadratic formula is straightforward. The coefficients (a = 2, b = -3, c = -5) are easily identifiable, and the formula can be applied directly to find the roots of the equation. This method is particularly advantageous for equations where factoring is not apparent or when completing the square is overly complex.
4. Clear Interpretation of Results
The quadratic formula not only simplifies the process of finding the roots but also provides a clear path to understanding the nature of these roots. By calculating the discriminant ((b^2 – 4ac)), we can immediately discern whether the roots are real and distinct, real and equal, or complex. This immediate insight into the nature of the solution is an added benefit of using the quadratic formula.
5. Educational Value
From an educational standpoint, the quadratic formula is a fundamental tool in algebra. Demonstrating its application in solving (2x^2 – 3x – 5 = 0) offers an excellent opportunity to reinforce its utility and show its effectiveness in solving a wide range of quadratic equations.
Step-by-Step Solution
To solve the quadratic equation (2x^2 – 3x – 5 = 0) using the quadratic formula, we will follow a systematic approach. The quadratic formula states that for any quadratic equation (ax^2 + bx + c = 0), the solutions for (x) can be found using the formula:
[ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} ]
Step 1: Identify the Coefficients
In our equation (2x^2 – 3x – 5 = 0), the coefficients are as follows:
- (a = 2), the coefficient of (x^2)
- (b = -3), the coefficient of (x)
- (c = -5), the constant term
Step 2: Substitute into the Quadratic Formula
Substitute these values into the quadratic formula:
[ x = \frac{-(-3) \pm \sqrt{(-3)^2 – 4 \times 2 \times (-5)}}{2 \times 2} ]
Step 3: Simplify the Expression
Now, simplify the expression step by step:
- Calculate the discriminant ((b^2 – 4ac)):
[ \sqrt{(-3)^2 – 4 \times 2 \times (-5)} = \sqrt{9 + 40} = \sqrt{49} ] - Simplify the numerator and the denominator:
[ x = \frac{3 \pm \sqrt{49}}{4} ] - Since (\sqrt{49} = 7), the expression becomes:
[ x = \frac{3 \pm 7}{4} ]
Step 4: Find the Roots
Now, solve for (x) using the plus and minus in the formula:
- For the ‘+’ sign:
[ x_1 = \frac{3 + 7}{4} = \frac{10}{4} = 2.5 ] - For the ‘-‘ sign:
[ x_2 = \frac{3 – 7}{4} = \frac{-4}{4} = -1 ]
Conclusion of the Solution
Thus, the equation (2x^2 – 3x – 5 = 0) has two real and distinct roots: (x_1 = 2.5) and (x_2 = -1).
Conclusion
In solving the quadratic equation (2x^2 – 3x – 5 = 0), we’ve effectively demonstrated the utility of the quadratic formula. This method not only provided the precise roots, (x_1 = 2.5) and (x_2 = -1), but also highlighted its applicability where simpler methods fall short. This exercise reaffirms the importance of understanding various mathematical approaches and their relevance in problem-solving. It serves as a vivid reminder of the elegance and enduring significance of mathematical principles in deciphering complex problems.